前言
这篇文章实在看完很多博客之后写的,需要读者至少拥有一定的CNN知识,当然我也不知道需要读者有什么水平,所以可能对一些很入门的基本的术语进行部分的解释,也有可能很多复杂的术语因为不好解释而没有解释(主要是懒)。看的时候最好结合论文和百度(谷歌、必应随意开心就好)。
ResNet简介
ResNet全称Deep residual network,中文名深度残差神经网络。因为ResNet在ImageNet等的优秀表现和出色的论文描述,作者何凯明获得了CVPR2016最佳论文奖。
论文原文地址:https://arxiv.org/pdf/1512.03385.pdf
顾名思义,ResNet的精髓在与深度和残差。深度是指模型的深度。在此之前,GoogleNet有22层,VGG有19层,AlexNet只有8层,但是ResNet有152层之多。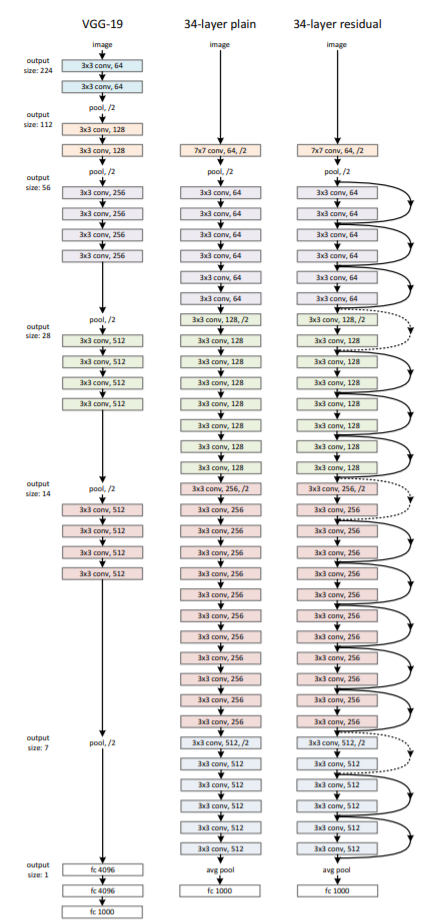
从网络层数和模型规模上来看,ResNet的规模远远大于之前的网络。ResNet取得的巨大成功从某种意义上确实源于深度。但是他在模型架构上还通过一种巧妙的方式解决了很多深度网络的问题,这就是残差学习(Residual learnning)。
ResNet的理论
深度学习的层数和训练效果存在必然的联系,从理论上来说,深度学习增加恒等映射层会获得比浅层模型更好地效果,因为从理论上浅层模型是更深层次模型解的一个子空间。但是咋实际中,我们经常会发现随着网络层数的增加,训练误差会上升,这当然不是因为过拟合(过拟合的训练误差会很低很低,相对的可能在验证集效果不好。)主要原因是因为梯度消失和梯度爆炸。这就是深度网络的退化问题。
梯度消失和梯度爆炸(这部分不喜欢可以跳过,我也是复制的)
梯度在高等数学中有了很详细的了解,我相信看这篇文章的铁汁集美也懂得什么叫反向传播,那么自然也就知道什么叫梯度消失和梯度爆炸,那我们是不是可以…(不是)。
好吧还是简单写(chao)一下吧。
反向传播:根据损失函数计算的误差通过反向传播的方式,指导深度网络参数的更新优化。
采取反向传播的原因:首先,深层网络由许多线性层和非线性层堆叠而来,每一层非线性层都可以视为是一个非线性函数(非线性来自于非线性激活函数,比如常用的Sigmoid、Tanh、ReLU…),因此整个深度网络可以视为是一个复合的非线性多元函数。
我们最终的目的是希望这个非线性函数很好的完成输入到输出之间的映射,也就是找到让损失函数(Loss function)取得极小值。所以最终的问题就变成了一个寻找函数最小值的问题,在数学上,很自然的就会想到使用梯度下降来解决。
什么?你说梯度下降是什么?额滴神啊!高数中是不是讲过函数的变化率沿着梯度方向变化的最快?我们举个栗子:
求函数的最小值。
- 求梯度:
- 向梯度的负方向移动特定的步长
- 好了又出来一个问题,对于一元函数,方向有两个:正方向和反方向,那么我们为什么往负方向走呢?这就需要泰勒公式来帮忙了。看下面的式子:
左侧是当前x移动一小步之后的下一个位置,他近似等于右边(球球了,泰勒展开不想讲了,自己看高数书吧)我们要找到一个方向,使
(我们要找最小值对吧),根据泰勒公式,显然我们需要另上式中的右侧加号后面小于0。
我们令阿尔法是一个很小的正数,这在机器学习和深度学习中叫做学习率(看到别人说学习率该知道是啥了)。
所以我们就能将公式进行替换确保。
下面就比较简单了,更新即可,这也就是所谓的沿负梯度方向更新。
回归正题,在梯度更新的过程中,以最简单的网络结构为例,加入有三个隐藏层,每层的神经元个数都是1,且对应的非线性函数为(其中为某个激活函数)如下图:
现在假设我们需要更新参数,那么我们就要求出损失函数对参数的导数,根据链式法则,可以写成下面这样:
而对于激活函数,之前一直使用Sigmoid函数,其函数图像成一个S型,如下所示,它会将正无穷到负无穷的数映射到0~1之间: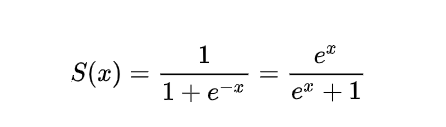
当我们对Sigmoid函数求导时,得到其结果如下:
由此可以得到它Sigmoid函数图像,呈现一个驼峰状(很像高斯函数)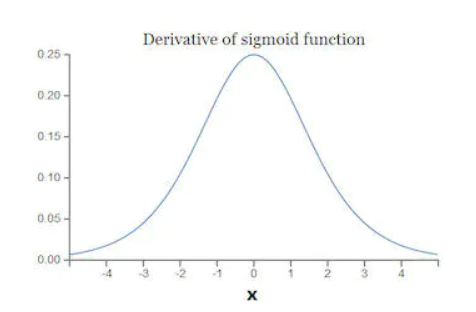
从求导结果可以看出,Sigmoid导数的取值范围在0~0.25之间,而我们初始化的网络权值通常都小于1,因此,当层数增多时,小于0的值不断相乘,最后就导致梯度消失的情况出现。同理,梯度爆炸的问题也就很明显了,就是当权值过大时,导致,最后大于1的值不断相乘,就会产生梯度爆炸。
残差学习是什么?
我们回到论文中的一张图片: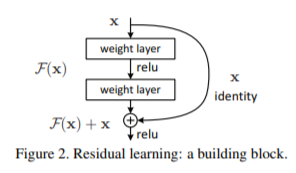
这是一个小块,定义是这样的:
这个小块有两个分支映射(mapping):
- identity mapping,指的是上图右边那条弯的曲线。顾名思义,identity mapping指的就是本身的映射,也就是自身;
- residual mapping,指的是另一条分支,也就是部分,这部分称为残差映射,也就是。
激活函数使用ReLU。
我们求得从浅层的学习特征为:
利用链式规则,可以求得反向过程的梯度:
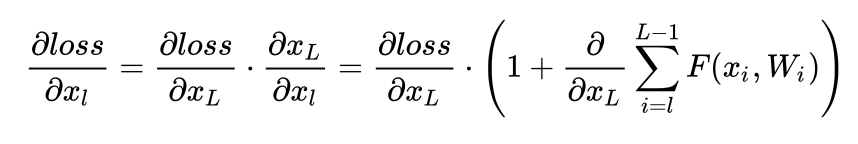
式子的第一个因子表示的损失函数到达的梯度,小括号中的1表明短路机制可以无损地传播梯度,而另外一项残差梯度则需要经过带有weights的层,梯度不是直接传递过来的。残差梯度不会那么巧全为-1,而且就算其比较小,有1的存在也不会导致梯度消失。所以残差学习会更容易。要注意上面的推导并不是严格的证明。
ResNet的网络结构
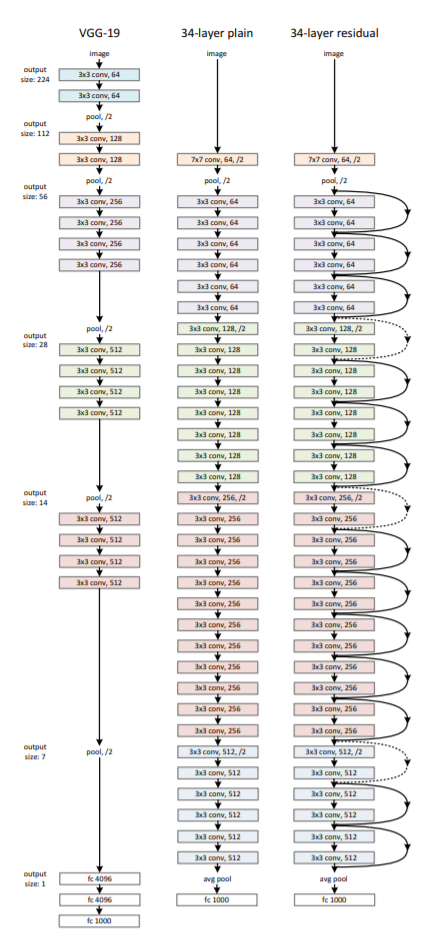
论文中给出了几种不同层次的网络结构,这里使用最简单的18层结构进行编码。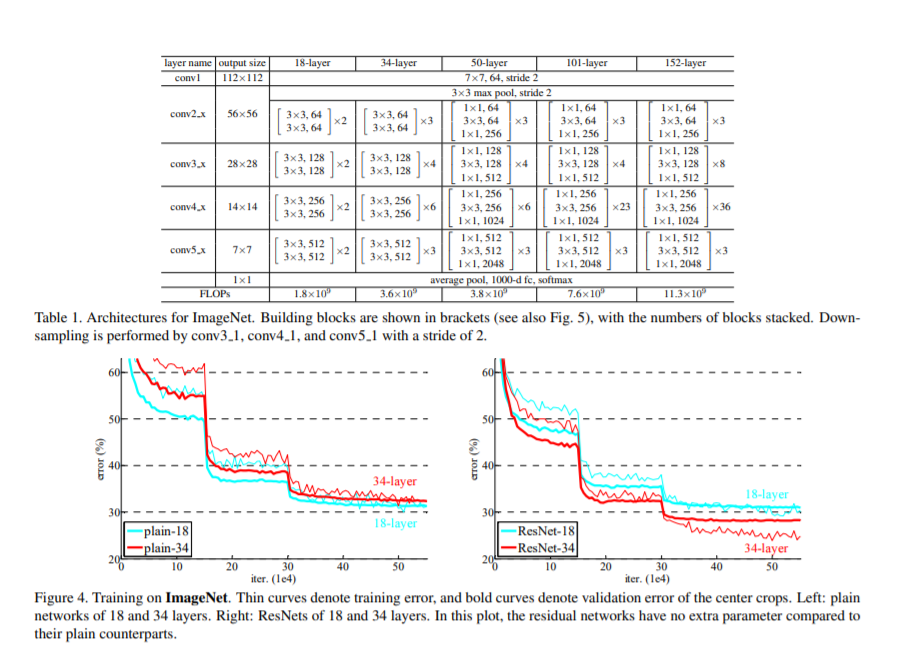

ResNet的18层模型构建代码:
1 | from keras.layers import Input |